Erwin Schrödinger proposed the famous thought experiment “the cat in an unobservable box,” also known as quantum superposition. He proved magnificent that we can’t be certain of a cat’s current status until we can not see it all. His experiment raises the question of when guessing about a cat’s life status ends, the probable reality becomes absolute reality. The experiment is known as Schrödinger’s.
Schrödinger’s Equation
Schrödinger’s equation is the Quantum Mechanical analog of Newton’s (1643-1727) second law of motion. The equation can be represented as:
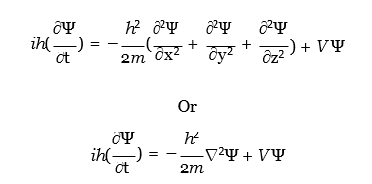
There are many ways of arriving at the equations of quantum mechanics. One way is by a variational approach using the work of J.L. Lagrange (1736-1813), the Italian “Giant,” or starting with the Hamiltonian and multiplying it by a complex wavefunction. Now, mentioning these names, in which direction should I go? Let’s stay with Hamilton (1805-65) for a moment; scholars state that during his honeymoon walking with his wife across the Broome Bridge in Ireland in 1843, he wrote down the expression for the multiplication of the quaternion separators i,j,k such that i2 = j2 = k2 =ijk = -1.
This was Hamilton’s eureka moment, comparable to Archimedes’s when he was shouting in the streets in Syracuse. I have been fortunate to discuss these quaternions during a course delivered at Oxford entitled Advanced Mathematics for Games Programmers, as three-dimensional transformations in Computer Games can be represented using them.
Different Approaches to Quantum Mechanics
Returning to Erwin, his approach of using a linear partial differential equation in Quantum Mechanics is not the only way of representing these systems. Other ways include the approach adopted by the “Giants” W. Heisenberg (1901-76) with his matrix mechanics after M.Born (1882-1970) realized that the non-commutative algebra that he was using was matrices.
Then there is the approach of the other legends R. Feynman (1918-88), who adopted the path integral formulation, and P.A.M Dirac (1902-84), who incorporated Special Relativity developed by A. Einstein (1879-55) in 1905 into Quantum Mechanics. Relativity has its roots in the work of Lorentz (1853-1928) and Fitzgerald (1851-1901), and it is perhaps a little-known fact that Einstein was almost piped to the Special Relativity summit by the enigmatic Henri Poincaré (1854-12) of his named conjecture fame which spawned the great Fields Medal controversy with G. Perelman (1966) who refused the prize, but that is for another day.
Conclusion
Staying with Relativity, this time with General, Albert was almost pipped to the post to this summit when he unwisely mentioned to Hilbert (1862-1943) (who, by the way, also advanced Quantum Mechanics) that he was having some Mathematical issues developing his Physics, which as it turned out was not the best thing to do, i.e., to state one’s Mathematical problems to arguably the greatest mathematician of the 20th century. I was again fortunate when I visited Göttingen to pay homage to the Prince of Mathematics J.C.F. Gauss (1777-1855) in 2009. I visited Hilbert’s tombstone and updated him that his 8th problem was still unresolved and that the Mathematics community was still working on it.
I reaffirmed Hilbert’s pledge by saying ” Wir müssen wissen wir werden wissen, (we must know we will know). D.Hilbert.
I have lost track of things again, and I should have mentioned Erwin’s cat, but I have run out of space; sorry, “Old friend.”


