Blog - Page 76 of 87

Jöns Jacob Berzelius: Father of the Swedish Modern Chemistry

Sci-Hub

-

November 2, 2023

Jöns Jacob Berzelius: Father of the Swedish Modern Chemistry

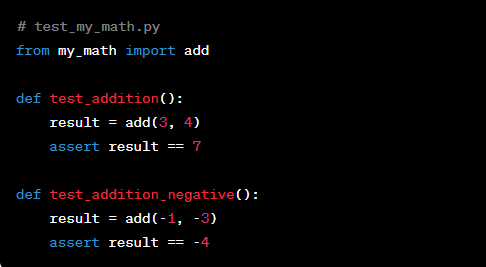
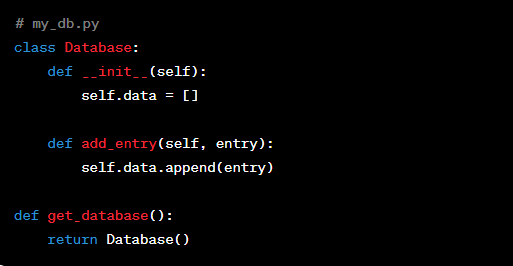
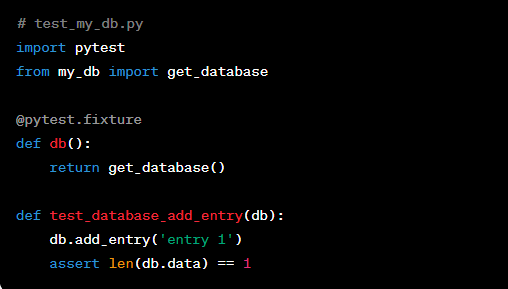
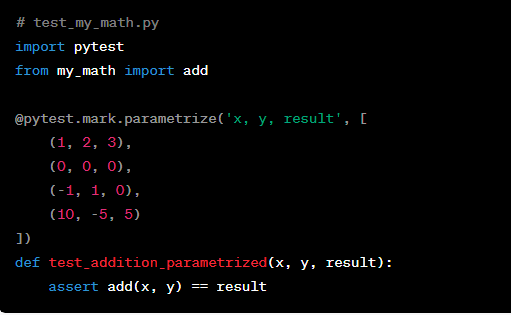
Jöns Jacob Berzelius, known as the Father of Modern Chemistry, was a Swedish scientist who made great contributions to the field of chemistry. Berzelius was born in 1779 in Väversunda, Sweden. Berzelius (1779-48) studied medicine at Uppsala University, but he increasingly devoted himself to chemistry. His careful tabulation of relative atomic weights led him to propose a basic principle of chemistry: that inorganic chemical compounds are always composed of atoms combined in whole number amounts. Berzelius also discovered several elements, including thorium and cerium. In Sweden, his birthday is honoured as Happy Berzelius Day!

Founders of Modern Chemistry

Jacob is in august company as Chemists go as he is considered in the same breath and same calibre as the likes of Robert Boyle (1627-91), John Dalton(1766-44), and Antoine Lavoisier (1743-94), to be one of the founders of modern chemistry. Boyle is also credited with being one of the founders of the Scientific Method which I have discussed in previous posts. His law relating the pressure, p, of a gas to its volume, v, such pv=constant (for a fixed mass of gas keeping the temperature constant) commemorates his greatness, but further reading reveals that he was also in possession of what we call Charles’ (1746-32) law, even though it was known to Gay Lussac (1778-50) before him.

Boyle rejected the presidency of the Royal Society and like many “Giants” of the time, his academic and professional career was greatly influenced by his religious views, another such “Giant” who springs to mind when I think of Science and religion is Michael Faraday (1791-67) who uttered one of the most prophetic of all quotes in Science which I would like to relay. After introducing electricity to Prime Minister Gladstone (1809-98) and trying to explain it, the conversation between the two of them goes like this:

Gladstone: “But, after all, what use is it?”
Faraday: “Why, sir, I know not, but I am sure one day you will be able to tax it!”

Chemistry Pioneers

Berzelius is also placed alongside Dalton who reintroduced the theory of the atom (first proposed by Democritus (c370BC)) as well as Lavoisier who is considered today the father of analytical Chemistry. No doubt we have all heard the story of Lagrange (1736-13) lamenting at Lavoisier’s beheading during the Reign of Terror of the French Revolution (1789-99) because he got himself embroiled with tax collectors. Below is the quote:

“Il ne leur a fallu qu’un moment pour faire tomber cette tête, et cent années peut-être ne suffiront pas pour en reproduire une semblable.” (“It took them only an instant to cut off this head, and one hundred years might not suffice to reproduce it’s like”).J.L.Lagrange.

Berzelius’s Law

Returning to Berzelius, he made advances in areas of Chemistry, including chemical bonding (covalent, ionic) and stoichiometry (which is related to quantities of reactants and products in chemical reactions) and his findings today are known as “The Law of Constant Proportions”.

I seem to have meandered off-piste again, and unfortunately, I have run out of space. Sorry, “old friend”.

Einstein’s Prediction of Gravitational Waves in Epic Black Holes

Sci-Hub

Dr Vasos Pavlika

-

November 2, 2023

0

Einstein’s Prediction of Gravitational Waves in Epic Black Holes

Einstein Predicted Gravitational Waves

On September 14, 2015, LIGO detected Gravitational waves, as predicted by Albert Einstein 100 years prior. These gravity waves (ripples in spacetime) are believed to result from a cataclysmic event calculated over a billion light years away. Physicists describe these waves as being produced in the final fraction of a second of a collision between two black holes merging into a single, more massive, spinning black hole. Some of the mass is converted into the energy of this gravitational wave given by E=mc².

Efforts to directly prove the existence of such waves had been ongoing for over fifty years and the waves are so small that Einstein doubted that they could ever be detected, but on Sept 14, 2015, LIGO made the first direct observation of gravitational waves with an instrument on Earth.

Unified Field Theory and the Forces of Nature

Albert made so many contributions to Modern Physics it was a shame that he parted company with the Quantum Physicists such as Planck (1858-47), Bohr (1885-62), Schrödinger (1887-61), Born(1882-70), Heisenberg (1901-76), Pauli (1900-58) etc in search of his Unified Field Theory, which attempts to combine the four fundamental forces of nature: the strong force, the weak force, the electromagnetic force, and the gravitational force. They work over different ranges and have different strengths. Gravity is the weakest, but it has an infinite range. The strong force binds quarks together in clusters to make more familiar subatomic particles, such as protons and neutrons. It also holds together the atomic nucleus. This force overcomes Coulomb’s repulsion.

The weak nuclear force acts inside of individual nucleons and has even shorter range than the strong force. It is the force that allows protons to turn into neutrons and vice versa. The electromagnetic force is the dominant force in the interactions of atoms and molecules and is mediated by photons. These two forces were elucidated by J. C. Maxwell (1831-79), who once worked at King’s College London, where I have been fortunate to study the gravitational force mediated by the so-called graviton. At present, we are still unable to reconcile the General Theory of Relativity (GR) with Quantum Physics at the instant of the Big Bang and thus GR is a classical theory.

The Sun’s Energy Production

Albert’s E=mc² explains how the sun sustains us. Inside our sun, atoms of hydrogen fuse (join) together to form helium, but the starting mass of hydrogen is greater than the mass of helium it produces, and this excess in mass is converted into energy according to E=mc², where c is the speed of light. Data suggests that the sun converts the equivalent of the mass of Mt Everest into helium every second, so we are talking about an immense amount of heat (stand in the mid-day sun in Saudi Arabia, and one can see how much power our star produces).

Not the best place to stop so abruptly, but I have run out of space again.

Until next time, “old friends”.

Efficient Python Testing: Best Testing Techniques with pytest

Artificial Intelligence

Syeda Umme Eman

-

November 2, 2023

0

Efficient Python Testing: Best Testing Techniques with pytest

Introduction:

An essential component of software development is testing. In addition to helping to guarantee that the code works as intended, it looks for any potential issues or flaws before they enter the system. Pytest is a well-liked testing framework in the Python community that offers an easy-to-use and efficient method for creating and executing tests.

What is Pytest?

A testing framework called Pytest makes it simple and scalable to create test cases. It is a flexible option for new and old projects because it can execute designed tests and is compatible with the integrated unit test framework.

Installing Pytest:

Installing Pytest can be done with the Python package management pip:

Writing Your First Test:

To begin, let’s create a basic Python function that we wish to evaluate. Take the process that adds two numbers, for instance:

Let’s now use Pytest to create a test for this function:

The assert statement used by the two test functions (test_addition and test_addition_negative) in the code above determines whether The outcome of the called add function is in line with expectations.

Running Tests:

To run the tests, you execute the pytest command in your terminal:

When a file is named test_ or ends in _test.py, pytest will automatically find it and run the test functions inside it.

Fixtures and Assertions:

Pytest supports many assertions that help you create clear, concise, and easy-to-read tests. It also has a strong fixture system for assembling and disassembling testing-related materials.

Let’s look at an instance when we need to post a more complex function:

We can write tests for this using fixtures:

The code above defines a fixture called db, which runs the get_database() function and returns a Database class instance. Afterwards, the test_database_add_entry method makes use of this fixture.

Parametrized Testing:

With Pytest, you can use parametrized testing to run the same test with different inputs. When testing a function with several data sets, this is helpful.

In this example, the @pytest.mark.parametrize decorator’s parameter sets cause the test_addition_parametrized function to be called four times, one for each possible combination.

Patching and Mocking:

You can easily construct mock objects for testing code that interacts with external services or dependencies by integrating pytest with the unittest.mock module.

Code Coverage:

Install the code-cov plugin to get reports on your test code coverage.

Then, run your tests with coverage using:

Conclusion:

Pytest is a robust testing framework that simplifies writing and executing Python tests. Due to its ease of use and adaptability, many developers favor it. You can guarantee the accuracy and dependability of your code by using pytest, which will ultimately result in more durable and maintainable software.

Albert Einstein and Marie Curie: Discussing the Lives of Two Giants

Sci-Hub

Dr Vasos Pavlika

-

November 1, 2023

0

Albert Einstein and Marie Curie: Discussing the Lives of Two Giants

I have been fortunate during my teaching career that has allowed me to teach and deliver seminars at many of the great universities around the world, including UCL, Oxford, Cambridge, the LSE, SOAS, Stanford, and UC Berkeley on many occasions, I have been allowed to discuss the lives and times of these two “Giants” of Science Marie Curie (1867-1934) and Albert Einstein (1879-1955). Starting with Einstein won the Nobel Prize in Physics in 1921 not for his work on Relativity but for his elucidation of the photoelectric effect by resurrecting Newton’s (1743- 1727) then dormant corpuscular theory of light (Huygens’s (1629-1695), Fresnel’s (1788- 1827) and Young’s (1773-1829 a polymath) wave theory is allowed to take center stage temporarily.

Einstein Papers That Revolutionized Physics

In 1905, Einstein whilst working a s a patent clerk third class, wrote four papers that would completely revolutionize the landscape of Physics and in so doing, elevate him to the dizzy heights of arguably the greatest Physicist of all time (perhaps only to be compared with Newton). Albert like Isaac before him also had a so-called miraculous year in 1666 during the plague years when he (Newton) retreated to Grantham and divulged his ideas that explained classical mechanics (that Aristotle (384-322BC)) had attempted to do and which Galileo (1564-1642) mastered and the theory of gravity by building on the three laws of Kepler (1571-1630) and the astronomical observations of Tycho Brahe (1546-1601, who died from a bladder infection due to his hedonistic lifestyle). Einstein’s four papers were on the Photoelectric effect, Brownian motion, Special relativity, and his immortal Mass-Energy relation.

Marie Curie Acheivements

I could go on talking about Albert in this entire post introducing his General Theory of Relativity, space-time, time dilation, the twin paradox, etc.

But let’s discuss Marie Curie (1867-1934) too. Marie was a Polish scientist who won two Nobel prizes, one with her husband Pierre (1859-1906) and the other with her daughter Irene (in Chemistry), and she is the only woman to date to have achieved this. Linus Pauling (1901-1994) also won two such prizes and would have most certainly won another if he had won the “race” in tracing the identity of DNA, but fortunately for Crick (1916-2004), Watson (1928-) and Wilkins (1916- 2004) he made an error in the interpretation of his results which opened the door for others whilst slamming the door tightly on the work of Rosalind Franklin (1920-1958) who once worked at Birkbeck College where I have been fortunate to teach.

Tragic End for Legend

Marie became the true alchemist, demonstrating how one element can be transformed into another with the discovery of radioactivity, thus fulfilling the quests of other alchemists, including Newton, Rutherford (1871-1937), and Avicena (980-1037AD). Regrettably, Marie’s life was cut short no doubt due to her exposure to radioactive materials. In fact, her notebooks are still radioactive and thus inaccessible to general viewing.

Alas, I have run out of space; perhaps I should write about each individually?

Richard Feynman: Numerical expert on the Manhattan Project

Sci-Hub

Dr Vasos Pavlika

-

November 1, 2023

0

Richard Feynman: Numerical expert on the Manhattan Project

Manhattan Project Race

Richard scored the highest ever MIT entrance exam, and like many of the others in the image, he won the Nobel Prize in Physics. Richard contributed to the Manhattan Project and was known to be the numerical expert there, quite a position to hold, especially when one considers that “Giants” like Fermi (1901-1954), Dirac of Fermi-Dirac statistics fame were also present, Dirac (1902-1984) by the way was Lucasian Professor of Mathematics at Cambridge.

Great Minds of Physics

Bohr (1885-1962) was also in attendance and combined Planck’s (1858-1947) ideas of quanta to explain the spectral lines of hydrogen (regrettably, his theory did not work for elements further in the Periodic table, i.e., with the higher atomic number), or even John Von Neumann (1903-1957, who was also present) and who as the last polymath contributed to modern Computer Science after Turing (1912-1954) and to Game theory after Nash (1928- 2015).

Returning once again to Feynman, I would like to recall a little anecdote about him that I always used to tell when I taught Quantum Electrodynamics (as I often say to my UCL students “during my previous life”). The story goes something like this: once, Feynman and his family were being heckled by some physicists in the US for driving their van with so-called Feynman diagrams painted on the outside of it, and one comment was said, “You can’t drive around with Feynman diagrams drawn on your van,” on exiting the van Richard is reported to have said, “Yes we can, we are the Feynmans.”

Famous C-Clamp Experiment

I particularly like the occasion when Richard determined the cause of the Challenger Disaster in which, during a hearing, Richard demonstrated the famous C-clamp experiment with the O-rings. Remaining with Feynman’s discussions, I also used to use the following lecture when discussing the Scientific Method and the work of Popper (1902-1904). Richard used to do much of his greatest thinking in Physics whilst visiting strip bars in the US, but this might be a good place to stop the discussion. Until next time.

Friedrich Bessel: Astronomer Journey with Prince of the Mathematics

Sci-Hub

Dr Vasos Pavlika

-

November 1, 2023

0

Friedrich Bessel: Astronomer Journey with Prince of the Mathematics

Friedrich Wilhelm Bessel was a collaborator of arguably the greatest Mathematician of all time, namely J.C.F. Gauss (1777-1855), the so-called “Prince of Mathematics,” who has the greatest quote in Mathematics and one that I think encompasses the lofty position that Mathematics must hold and which I often quote verbatim during my lectures:

“Arithmetic is the Queen of Mathematics, and Mathematics is the Queen of the Sciences; she often condescends to render service to Astronomy and other natural sciences, but under all circumstances, the first place is her due” J.C.F. Gauss.

Tribute to Prince of Mathematics and Bessel

When Gauss mentions arithmetic here, he is referring to the study of primes, which is, of course, limitless, as demonstrated by the great Greek ”Giant” Euclid (300BC) and author of the immortal Elements. I say limitless because when there is an announcement that the largest prime has been determined, there are still infinitely more (that is the strangeness of Mathematical infinity), so one can keep searching forever, and we will continue to find them; their frequency becomes less dense as the size of the prime increases but there is still infinity of them yet to find. The Bessel functions named in his honor arising from the solution of his namesake differential equation were known to Daniel Bernoulli (1700-82), one of the 8 great Bernoulli men (who, by the way, did not get on due to their competitiveness as to who was the greatest).

Bernoulli’s Legacy

Daniel gave us his conservation of energy equation that allowed mankind to realize his/her dream that flight is possible with his immortal equation. Jakob Bernoulli (1655- 1705) first proved the “Law of large numbers,” on which all probability theory depends, so quite an august family. Returning to Bessel along with his equation, he generated the Bessel- Gauss beam for application to optical beams. In January 1810, Bessel was appointed director of the newly founded Konigsberg Observatory. Bessel was a skilled astronomical observer, and he is probably best remembered for being the first to determine a stellar parallax reliably.

Maths Giants and Legends

In 1842 Bessel met C. G.J. Jacobi (1804-51), who was the second most prolific Mathematician of all time (second to L. Euler (1707-83)). At UCL, I often teach the Gauss-Seidel and the Gauss-Jacobi methods, and when I do, I discuss these ”Giants,” which I believe my students enjoy. I then also go on to teach the Cayley-Hamilton theorem, taking the opportunity to talk about W. Hamilton (1805-65), mentioning that his amorous advances to William Wordsworth’s sister were curtailed after Wordsworth read one of his poems of amour advising him that he was not a poet and that he should devote his efforts to Mathematics. Of course, Hamilton’s incident on the Broom Bridge during his honeymoon concerning the multiplication of quaternions is legendary, but that is for another post.

Alas, again, I have run out of space.

Gustav Ludwig Hertz: Discovery of the Discrete Energy

Sci-Hub

Dr Vasos Pavlika

-

October 31, 2023

0

Gustav Ludwig Hertz: Discovery of the Discrete Energy

Discrete Nature of Energy

Gustav demonstrated that energy is absorbed by an atom only in discrete amounts, quanta. This was not the first time energy was considered to consist of discrete packets of energy. Recently, I discussed Einstein’s (1879’-1955) photoelectric effect, which suggests that to explain the experimental results, one must consider the radiation as a particle (a photon) with energy hf, (h is Planck’s constant and f the frequency of radiation). This energy is then used to overcome the attraction between the electron and the atom whilst providing kinetic energy to the emitted electrons, so a beautiful exposition of the conversation of energy law.

Bohr-Einstein Debates

This idea was further used by Compton (1892-1962) when scattering X-rays with electrons, the change in wavelength before and after scattering is measured, and this allows for the change in energy to be determined and measurements of the energy of the scattered photon allows for a demonstration once again of the conversation of energy. We can do this with all forms of radiation due to de Broglie’s (relation) p =c/hf, where p=momentum, c is the speed of light. This result also explains why we do not diffract when we walk through a door, as with our momentum the aperture must be 10⁻32m.

Einstein, by the way was a big fan of de Broglie; this was before Einstein took objection to the probabilistic approach of Quantum Physics with the emergence of the Bohr-Einstein debates which are now legendary, especially during the most famous gathering of the greatest Physical minds at the 1926 Solvay conference where 17 of the 29 attendees won Nobel prizes (Marie Curie won two). During these so-called Bohr-Einstein debates, we have the famous utterings:

Einstein: God does not place dice with the Universe.

Bohr: Stop telling God what to do.

Battle of Three Giants

Einstein’s attempt to dismantle the Heisenberg (1901-1976) Uncertainty Principle culminated in the famed thought EPR experiment, but once again, Bohr won the battle, and only time will tell if he won the war. Scholars suggest that whilst Heisenberg was made head of nuclear research for Germany during WWII, he deliberated stalled advances in nuclear research to prevent Germany from having a weapon of mass disruption. If this is the case, he can be considered a war hero, just like the Mathematical code-breakers led by Turing (1912-1954).

Hertz’s Studies & Contribution

Returning to Hertz, he studied at the once center of the Mathematical and Physical world, Gottingen, having among its staff Ludwig Prandtl (of the Prandtl-Meyer expansion (supersonic flow around a convex corner), Carl Friedrich Gauss (1777-1855) known as the Prince of Mathematics, Bernhard Riemann (1826-1866), of the Riemann Hypothesis fame, and Peter Gustav Lejeune Dirichlet (1805-1859) who was the first successor of Gauss and contributed to Fourier series and the study of partial differential equations.

Alas, once again I have run out of space and must end here.

Fintech: Principles for Sustainable Growth

Syeda Umme Eman

-

October 31, 2023

0

Fintech: Principles for Sustainable Growth

Introduction:

Financial technology, or fintech for short, is a quickly developing industry that combines innovation and technology to change how financial services are provided and used. Fintech, which includes mobile banking and cryptocurrencies, has upended traditional finance and spurred innovation. The following core principles form the basis of the fintech revolution:

1. Client-First Mentality:

A significant emphasis on the client is one of the fundamental tenets of fintech. Fintech businesses work hard to comprehend the requirements and problems of their users to create solutions that meet their needs. This customer-centric approach informs the design and development of personalized experiences, user-friendly applications, and straightforward interfaces.

2. Disruption and Innovation:

Innovation is essential to fintech. It aims to question and upend established financial institutions and concepts. Fintech businesses use cutting-edge technology like blockchain, AI, and big data analytics to provide innovative solutions that help optimize workflows, cut expenses, and boost productivity across various financial services.

3. Solutions Driven by Technology:

Technology is at the heart of fintech. Technology is the driving force behind fintech innovation, whether in the form of blockchain technology for safe transactions, automated investment algorithms, or mobile banking apps. Fintech businesses can provide innovative answers to financial problems using recent technological developments.

4. Adherence to Regulations:

Fintech operates in a highly regulated environment despite its disruptive nature. Respecting regulatory frameworks and compliance requirements is essential to building credibility and guaranteeing the security and stability of financial institutions. To traverse the complicated legal frameworks, fintech companies need to collaborate closely with regulatory organizations.

5. Privacy and Security of Data:

The increasing prevalence of digital transactions highlights the critical need to protect sensitive financial data. Fintech businesses invest significantly in strong cybersecurity defenses to shield consumer data from threats like hacking and illegal access. Adherence to data protection laws, such as the General Data Protection Regulation (GDPR), is paramount.

6. Monetary Inclusion:

Fintech can close access gaps in the financial services industry and give previously marginalized or excluded groups of people access. Fintech companies want to democratize finance and guarantee that a wider range of people and businesses can participate in the global economy by using technology to provide more inclusive solutions.

7. Blockchain & Distributed Ledger Technology:

A key component of the fintech blockchain is a decentralized ledger system. Peer-to-peer transactions are made possible by it, which are essential to cryptocurrencies and several other financial applications.

8. Collaborations and Environments:

Fintech businesses frequently work with other startups, traditional financial institutions, and stakeholders in the larger ecosystem. These collaborations may result in synergies that broaden the use and effect of fintech solutions while facilitating the integration of complementary services and technologies.

9. Ethical and Responsible Practises:

Fintech businesses are under growing pressure to operate morally and responsibly towards society. It can involve considering ethical lending procedures, fee transparency, and long-term financial solutions.

10. Reliability:

Fintech businesses seek solutions that expand effectively and quickly. Long-term success depends on your capacity to support an expanding user population while keeping performance and dependability high. Modular designs, cloud computing, and effective resource management are frequently used to achieve scalability.

11. Ongoing Education and Adjustment:

The fintech industry is dynamic, with new trends and technology appearing regularly. Fintech businesses must cultivate a culture of ongoing education, flexibility, and agility. They can react swiftly to shifting consumer demands and changing regulatory landscapes by being on the cutting edge of industry advancements.

Conclusion:

The concepts put forth here form the foundation of the fintech revolution. By following these guidelines, fintech businesses are revolutionizing the financial sector, creating creative fixes, and enhancing global accessibility to financial services. The potential for more transformational change in the financial industry is limitless as technology develops.

Robert Hooke: Enemy of the Isaac Newton

Sci-Hub

Dr Vasos Pavlika

-

October 31, 2023

0

Robert Hooke Empirical Law

I would like to pay homage to an unsung hero of Science Robert Hooke (1635-1703) who had the misfortune of making an enemy of Isaac Newton (1642-1726) which to say the least was not best thing to do. Posterity will recollect that Hooke is credited with the law that bears his name (Hooke’s law) that one learns as a young Physics student but quite frankly, this is not the most flattering law.

Hooke’s Law
Hooke’s Law explains the relationship between force, distance, and deformation of objects (i.e., compression or extension). The law notes that the required force to compress or extend an object is linearly proportional to the distance. Therefore, to move an object in an direction, by force x, then as the distance doubles, force may also be estimated as 2X. Therefore, we can use the distance as contact (k) We can state the law as F_s = kx.

Contribution to Math and Science

Hooke is also credited for observing microorganisms, creating his famed micrographia (small drawings) in which he coined the term ”cell” for biological cells as what he observed, as he put it, reminded him of prison cells.

Hooke was educated at Oxford, and there is today the Robert Hooke Building (Cambridge having the Isaac Newton Institute); Hooke was a polymath and the 9th Gresham Professor. I have been fortunate to meet and work with many such professors, including Raymond Flood (Oxford line manager) and Robin Wilson (son of the late PM, Harold), who delivered talks at an LSE Summer school in Mathematics that I used to direct. I have also been fortunate to discuss Mathematics with another Gresham Professor, namely Christopher Zeeman(1925-2016), again at Oxford after he gave an impromptu talk on Euclid during a History of Mathematics symposium.

Returning to Hooke, he postulated the inverse square law of gravity, but alas he was not as Mathematically competent as Newton, who used the three laws of planetary motion of Kepler (1571-1830) and was able to Mathematically verify that only with an inverse square law could one arrive at elliptical planetary orbits. Hooke also helped Boyle (1627-1691) with his gas experiments, arriving at the so-called Boyle’s law of ideal gases. Hooke also worked with Wren (1632-1723) after the great fire of London.

Robert Hooke Confronts Newton

Hooke and Newton did temporarily reconcile their differences but remained mortal enemies during the later parts of their lives so much so that Newton had every portrait of Hooke at the Royal Society burnt. Newton was quite a would-be arsonist, and it is perhaps well known as a teen, he made a list of his past sins such as: “Threatening my father and mother Smith to burn them and the house over them.”

The legendary quote often attributed to Newton, which many authors believe demonstrates Newton’s magnanimity, is:

“If I have seen further [than others], it is by standing on the shoulders of giants – I. Newton.”

However, this quote is nothing of the kind, it was a direct attack on Hooke as he was short and a hunchback, so Newton was being cruel on two counts. In 1686, when the first book of Newton’s Principia was presented to the Royal Society, Hooke claimed that he had prompted Newton with the idea of Gravity, advising him that:

”The rule of the decrease of Gravity, being reciprocally as the squares of the distances from the Center”.

Isn’t it just beautiful how these giants enunciated their laws in this case the inverse square law?

Alas, once again, I have run out of space and must end here.

Carl Anderson – Discovery of the Positively Charged Electron

Sci-Hub

Dr Vasos Pavlika

-

October 31, 2023

0

Carl Anderson – Discovery of the Positively Charged Electron

Positron Discovery

Anderson’s (1905-91) discovery of the positively charged electron was a groundbreaking achievement that revolutionized the field of physics. Anderson worked with the ”Giant” Robert Millikan (1868-1953) of the famed Millikan oil drop experiment in which an electron is held stationary in an electric field, and by equating the electric force with the gravitational force, one arrives at the formula q=mgV/d, where d is the distance between the plates and V the potential difference, other symbols having their usual meaning and q can then be determined.

The Photoelectric Effect

Remaining with Millikan for a moment, he carried out experimental work on the Photoelectric effect, verifying Einstein’s expression (and thus his interpretation) of the phenomenon and, in so doing, accurately determined Planck’s (1858-1947) constant. Not a bad mentor to have for young Anderson. But this reminds me of one of the most beautiful quotes in Science (In fact, it was said by a Mathematician, but I think it is equally valid in the Sciences):

“It appears that to progress in Mathematics; one must study the Master and not the pupils- N.H.Abel”

I wrote this on the copy of my Ph.D. thesis that I sent to my late Ph.D. advisor (may he rest in peace) with the additional remark. I said that the quote was not sufficiently general and that one could insert the word ”with” after the word ”study.”

Anderson, like Rutherford (1871-1937) before him, was a great experimentalist. Both legends were able to not only perform these epoch-making experiments but also to explain the governing theory behind them.

Uncovering the Fascinating World of Physics

Anderson was able to detect a muon and thus was a pivotal figure in the elucidation of the standard theory of elementary particle Physics in this case of a lepton; I could at this point start discussing Bosons and up/down quarks and thus mention people like Bose (1894-1974) and Fermi (1901-54), but that would lead me too far astray. It is interesting to note that the word lepton from the Greek for thin (calling someone leptin in Greek is guaranteed to raise a smile) is also used in Statistics when describing probability distributions (leptokurtic).

Conversely, one would not describe someone as platy in Greek (platykurtic (fat), for fear of unwanted advances). Anderson thought that he had discovered a pion and that he had thus verified the work of Yukawa (1907-81), which is the particle involved in the ”strong force”…. Alas, I have run out of space again.

Masketer

Masketer

Masketer

Company

Masketer

Masketer

Founders of Modern Chemistry