Bonds Pricing
Bonds are dynamically priced financial instruments. When they are issued initially, their price is indicated by their par value (or face value); however, later, the value of bonds is subject to factors such as the interest rate, credit ratings of the issue, liquidity in the market, or general economic and business aspects. Therefore, when buying bonds, investors need to carefully understand the theoretical price of the bonds and the possible implications of exogenous factors on the cost of a Bond.
Bonds’ Cash Flows
Bonds are long-term financial assets (debt instruments). The cash flows associated with these instruments are a time-based phenomenon. A bond investor, in essence, incurs a cash (£) outflow today to receive interest income and principal payments in future (Inflows). The example below explains the cash inflows and outflows associated with a bond maturing in 3 years, a par value of £1000, and an annual interest rate of 10%. The bond pays interest semi-annually; hence, the bond investor will receive £50 every 6 months. t0 means today, t1 means in six months, t2 means in 12 months, and so on (please see the picture below).

Source: Author’s creation.
Therefore, a bond purchase is an exchange of money today against promised money in the future. Accordingly, to find a bond’s value (price), we must calculate the present value of these future cash inflows (as depicted below).
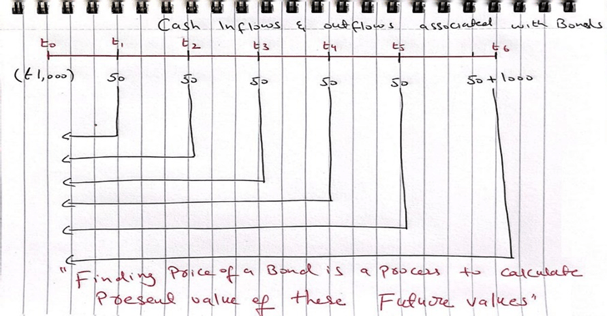
Source: Author’s creation.
The bond valuation can be done using the following formula.
![]()
- Coupon payment = Interest rate offered by the bond.
- [coupon payments are calculated by considering if they are paid annually, semi-annually, or quarterly]. For example, an annual interest rate of 10% means a 5% semi-annual rate, which is calculated as 10%/2. If it was monthly, then we divided 10% by 12.
- r = discount date or required rate of return by the company.
- n = periods to maturity.
- Principal payment = par value, which the investor paid at the beginning.
Another way of approaching this is the following equation, where we discount all the cash flows individually and then sum up the discounted cash inflows to estimate the present value of future cash flows.
![]()
Example:
| Bond A | Bond B | |
| Maturity (years) | 50 | 20 |
| Coupon rate (%) | 9 | 8 |
| The interest rate paid on the principal (paid semiannually) | ||
| Par Value/Face Value/Book Value | $1,000 | $1,000 |
Find price and tell whether they are selling at premium or discount.
Solution:
Price of Bond A
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Price of Bond B
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Both bonds are selling at a discount value.
Principles of Bond Pricing
The price of a bond is the function of the future cash flows associated with the bonds and their certainty. The first requires bond issuer to offer a rate that is better than the alternative investment rate (required rate of return). The second refers towards default risk premium.
The required rate of return discounts the future cash flows to the present to establish their present value. Therefore, the present value of cash flows associated with a directly depends upon the discount rate (required rate of the investors). Therefore, the discount rate is the primary determinant of the value of the bonds. The relationship between bond prices and the required rate is inverse. As the required rate goes up, the price of the bond decreases.
However, the question of how this required rate is determined. This rate is determined by the interest rate set by the Bank of England in the UK or the Federal Reserve Bank in the USA. This rate is also known as the risk-free rate and is one of the most important variables in our economy.
Furthermore, it’s also important to remember that the relationship between risk-free rates and bond prices is inverse; as the interest rate increases, the bond price decreases. Risk free rate of a country is influenced following four forces:
- Inflation Levels and future expectations about inflation levels. The higher the inflation level and future expectations, the higher the risk-free rate.
- Economic Growth or national levels of output. The slower the Growth, the lower the risk-free rate, and vice versa.
- Quantity supply of money or, in other words, how much money the Bank of England prints. The relationship is convex and shows the complexity and sensitivity with which central banks need to deal with this problem.
- Fiscal situation of a country. Suppose a country is in deficit and needs to borrow more money. As a result, the risk-free rate increases and vice versa.
Default Risk Premium refers to the credit risk associated with a bond issuer. The risk indicates whether an issuer can make the promised future payments on time. This risk depends on an issuer’s ability to generate revenues or sales. An issuer in a growing economy is more likely to make future payments and vice versa. Therefore, Bond issuers must offer an interest rate that compensates for default risk or may have to sell the bond at a discount.
References
- Mishkin, F. S., & Eakins, S. G. (2019). Financial markets. Pearson Italia.
- Madura, J. (2020). Financial markets & institutions. Cengage learning.
- Pilbeam, K. (2023). International finance. Bloomsbury Publishing.
- Fabozzi, F. J., Modigliani, F., & Jones, F. J. (2010). Foundations of financial markets and institutions. Pearson/Addison-Wesley.
- Kaufman, H. (1994). Structural changes in the financial markets: economic and policy significance. Economic Review-Federal Reserve Bank of Kansas City, 79, 5-5.
- Kaufman, H. (2009). The road to financial reformation: Warnings, consequences, reforms. John Wiley & Sons.
- Kaufman, H. (2017). Tectonic Shifts in Financial Markets: People, Policies, and Institutions. Springer.
- Hunter, W. C., Kaufman, G. G., & Krueger, T. H. (Eds.). (2012). The Asian financial crisis: origins, implications, and solutions. Springer Science & Business Media.
- Glushchenko, M., Hodasevich, N., & Kaufman, N. (2019). Innovative financial technologies as a factor of competitiveness in the banking. In SHS Web of Conferences (Vol. 69, p. 00043). EDP Sciences.
- Kaufman, G. G. (2002). Too big to fail in banking: What remains?. Quarterly Review of Economics & Finance, 42(3), 423-423.
- Kaufman, G. G. (2000). Banking and currency crises and systemic risk: Lessons from recent events. Economic Perspectives, 24(3), 9-28.
- Diamond, D. W., Kashyap, A. K., & Rajan, R. G. (2017). Banking and the evolving objectives of bank regulation. Journal of Political Economy, 125(6), 1812-1825.

