Blog - Page 77 of 87

Pythonic DS and Algorithmic Paradigms: A Practical Approach

Artificial Intelligence

-

October 30, 2023

Pythonic DS and Algorithmic Paradigms: A Practical Approach

Introduction:

The fundamental concepts of computer science, specifically data structures and algorithms, provide the basis for efficient software development. They offer a systematic approach to data organization, manipulation, and storage, facilitating effective problem-solving across various industries. Python is a well-liked and flexible programming language that supports many techniques and has a robust built-in data structure library. We’ll look at some of the most important Python data structures and algorithms in this article.

Data Structures in Python

1. Lists:

One of the most useful and popular data structures in Python is the list. These are ordered collections of items that can hold any data type, including text, integers, and other lists.

2. Tuples:

The similarity between tuples and lists is that once a tuple is created, it can’t change. When portraying fixed sets of data, they are helpful.

3. Sets:

Unsorted groups with distinct components are called sets. They are handy for assignments that call for membership testing or typical values.

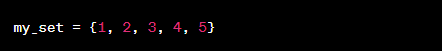
4. Dictionaries:

Key-value pair groupings make up dictionaries. They are frequently used for data retrieval and offer quick lookup based on keys.

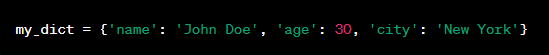
5. Linked Lists:

A linked list comprises nodes, each with a value and a reference to the node after it. They are especially helpful when putting dynamic data structures into practice.

6. Stacks and Queues:

Stacks follow the Last-In, First-Out (LIFO) principle, while queues follow the First-In, First-Out (FIFO) principle. They are essential for managing data in a structured way.

7. Trees:

Trees are hierarchical data structures composed of nodes. They find applications in various fields, including databases, file systems, and AI.

8. Graphs:

Graphs consist of nodes and edges that connect them. They are fundamental in modeling relationships and networks, such as social networks or road maps.

Algorithms in Python

1. Sorting Algorithms:

Data is arranged in a specific order via sorting algorithms. Typical sorting formulas consist of the following:

Bubble Sort
Selection Sort
Insertion Sort
Merge Sort
Quick Sort

2. Searching Algorithms:

Algorithms for searching find particular data inside a collection. Typical search algorithms consist of:

Linear Search
Binary Search
Hashing Algorithms

3. Recursion:

Recursion is a problem-solving strategy in which a function calls itself. Algorithms for dynamic programming and tree traversal tasks make extensive use of it.

4. Modular Programming:

By dividing a problem into smaller, more manageable subproblems, dynamic programming is an effective problem-solving method. It is applied to optimization issues like the knapsack issue.

5. Graph Algorithms:

Graph algorithms handle graph-related operations such as traversing, shortest path searching, and cycle detection. Among the notable algorithms are:

Breadth-First Search (BFS)
Depth-First Search (DFS)
Dijkstra’s Algorithm
Bellman-Ford Algorithm

Conclusion:

Python is a great option for many applications because of its large support for algorithms and comprehensive collection of data structures. Writing scalable and efficient code requires an understanding of these ideas and the ability to determine which data structure or method to employ at what time. With the information in this article, you will be more capable of taking on challenging issues and creating reliable Python software solutions. To become an expert programmer, keep learning, using, and refining these ideas.

Understanding the Internal Rate of Return: Accountant’s Perspective

Finance

Faisal Sheikh

-

October 30, 2023

0

Understanding the Internal Rate of Return: Accountant’s Perspective

Accountants, despite their contempt for finance, are incomplete without understanding the concepts of finance. Internal Rate of Return is one such concept that every accounting student must learn, irrespective of the level of their education. In this short article, I will attempt to demystify the IRR by discussing why an organization should consider calculating it and, crucially, how it is utilized in Corporate Finance.

Defining Internal Rate of Return

I am currently teaching a final-year undergraduate class in Corporate Finance. I remain in awe of the versatility of the IRR. However, many of my students would beg to differ!

IRR is an important financial indicator in Corporate Finance for assessing the profitability and desirability of investment initiatives, including capital expenditures, acquisitions, and new product development. It’s an immensely powerful decision-making technique, highlighting the annualized rate at which an investment breaks even or where Total Revenue equals Total Costs.

We can also define it as a discount rate that, throughout an investment, compares the present value of cash inflows to the initial investment (the present value of cash outflows). Put more, it is the pace at which an investment’s net present value (NPV) falls to zero. It is also important to note that the IRR represents the expected return on investment.

Why Do We Calculate IRR?

Investment Appraisal: Assessing the viability of investment projects is one of the main purposes of computing IRR. A greater internal rate of return (IRR) suggests a potentially more appealing investment when comparing multiple projects. Businesses use this statistic to determine which projects to accept and which to refuse.
Capital Budgeting: When a business divides resources among several investment options, IRR is a key factor. An organization can prioritize and choose initiatives anticipated to yield the highest profits by evaluating the IRR of different projects.
Risk Assessment: The timing and magnitude of cash flows are also considered by IRR. Usually, the project with the earliest cash flows is favored when two projects have the same estimated return. This is especially crucial when considering the time value of money and the unpredictability of future cash flows.
Comparing Investments: When comparing investments of varying sizes, durations, and cash flow patterns, IRR is a helpful tool. Since it permits an ‘apples-to-apples’ comparison and aids in standardizing the evaluation procedure.
Internal Benchmarking: An organization can use IRR as an internal benchmark to assess how well its investments are performing and how well it is performing overall. A business is creating value if it regularly generates IRRs higher than its cost of capital.

Internal Rate of Return for Managers

Capital Allocation: An important consideration in a company’s financial resource allocation is its IRR. A business can decide where to invest its limited cash to maximise returns by evaluating IRRs.
Project Selection: IRR assists a corporation in identifying the most financially appealing projects within its pool of investment alternatives. It directs management in selecting initiatives or projects that maximize returns while congruent with a company’s strategic goals or objectives.
Merger and Acquisition (M&A) Decisions: In M&A deals, the IRR is an essential calculation. Since purchasing a business entails a substantial initial outlay, the IRR aids in determining if the projected future cash flows from the deal will balance this out.
New Product Development: Businesses spend money on R&D to produce new goods or services. IRR is used to rank which products are worth pursuing and to evaluate the projects’ financial viability.
Cost of Capital Estimation: An organization’s cost of capital and IRR are strongly correlated. A corporation can ascertain if a project is likely to create or destroy value by comparing its IRR to its cost of capital.
Real Estate Investments: IRR is a widely used metric to assess real estate investments. It determines the attractiveness of a real estate investment by considering the acquisition cost, rental income, and projected future appreciation.
Asset Replacement Decisions: IRR assists in determining if it is financially prudent to replace outdated or inefficient equipment or assets with newer, more efficient alternatives.

Conclusion

To sum up, one of the most important tools in Corporate Finance is the Internal Rate of Return or IRR. It enables businesses to evaluate financial viability, deploy money effectively, make superior choices regarding capital budgeting, better assess mergers and acquisitions, explore product developments, and other areas. It allows businesses to maximize shareholder value and accomplish their strategic goals by computing and comparing IRRs.

Finally, IRR remains a useful indicator; however, to obtain optimal results and ensure robust decision-making, it should be used with other financial metrics and the context of a company’s unique financial objectives and risk tolerance.

In my next article, I will explore my love for the Capital Asset Pricing Model, AKA CAPM…

Erwin Schrödinger’s Equation – Is the Cat Dead or Alive?

Sci-Hub

Dr Vasos Pavlika

-

October 30, 2023

0

Erwin Schrödinger proposed the famous thought experiment “the cat in an unobservable box,” also known as quantum superposition. He proved magnificent that we can’t be certain of a cat’s current status until we can not see it all. His experiment raises the question of when guessing about a cat’s life status ends, the probable reality becomes absolute reality. The experiment is known as Schrödinger’s.

Schrödinger’s Equation

Schrödinger’s equation is the Quantum Mechanical analog of Newton’s (1643-1727) second law of motion. The equation can be represented as:

There are many ways of arriving at the equations of quantum mechanics. One way is by a variational approach using the work of J.L. Lagrange (1736-1813), the Italian “Giant,” or starting with the Hamiltonian and multiplying it by a complex wavefunction. Now, mentioning these names, in which direction should I go? Let’s stay with Hamilton (1805-65) for a moment; scholars state that during his honeymoon walking with his wife across the Broome Bridge in Ireland in 1843, he wrote down the expression for the multiplication of the quaternion separators i,j,k such that i² = j² = k² =ijk = -1.

This was Hamilton’s eureka moment, comparable to Archimedes’s when he was shouting in the streets in Syracuse. I have been fortunate to discuss these quaternions during a course delivered at Oxford entitled Advanced Mathematics for Games Programmers, as three-dimensional transformations in Computer Games can be represented using them.

Different Approaches to Quantum Mechanics

Returning to Erwin, his approach of using a linear partial differential equation in Quantum Mechanics is not the only way of representing these systems. Other ways include the approach adopted by the “Giants” W. Heisenberg (1901-76) with his matrix mechanics after M.Born (1882-1970) realized that the non-commutative algebra that he was using was matrices.

Then there is the approach of the other legends R. Feynman (1918-88), who adopted the path integral formulation, and P.A.M Dirac (1902-84), who incorporated Special Relativity developed by A. Einstein (1879-55) in 1905 into Quantum Mechanics. Relativity has its roots in the work of Lorentz (1853-1928) and Fitzgerald (1851-1901), and it is perhaps a little-known fact that Einstein was almost piped to the Special Relativity summit by the enigmatic Henri Poincaré (1854-12) of his named conjecture fame which spawned the great Fields Medal controversy with G. Perelman (1966) who refused the prize, but that is for another day.

Conclusion

Staying with Relativity, this time with General, Albert was almost pipped to the post to this summit when he unwisely mentioned to Hilbert (1862-1943) (who, by the way, also advanced Quantum Mechanics) that he was having some Mathematical issues developing his Physics, which as it turned out was not the best thing to do, i.e., to state one’s Mathematical problems to arguably the greatest mathematician of the 20th century. I was again fortunate when I visited Göttingen to pay homage to the Prince of Mathematics J.C.F. Gauss (1777-1855) in 2009. I visited Hilbert’s tombstone and updated him that his 8th problem was still unresolved and that the Mathematics community was still working on it.

I reaffirmed Hilbert’s pledge by saying ” Wir müssen wissen wir werden wissen, (we must know we will know). D.Hilbert.

I have lost track of things again, and I should have mentioned Erwin’s cat, but I have run out of space; sorry, “Old friend.”

Stokes, “The Man Who Understood Fluid Mechanics”

Sci-Hub

Dr Vasos Pavlika

-

October 30, 2023

0

Stokes, “The Man Who Understood Fluid Mechanics”

Stokes introduced us to the fluid world of Fluid Mechanics and how Fluids move. However, my relationship with Gabriel Stokes is divine. It was during a lecture on his work that I could showcase my understanding of Physics.

Career Shaping Work of Stokes

I recall an event regarding this equation that shaped my professional career; it goes something like this. I attended a History of Mathematics conference in March 2004 at Oxford University. There was an eminent speaker, Ivan Grattan Guinness (1941-14), giving a talk on the Navier-Stokes equation.

During his talk, it occurred to me that he had mentioned everyone important in its development except the person I thought was fundamental (in this case, Newton). During the Q&A, I mentioned to him that the most important protagonist had been omitted. He replied to me, “Who was that?”. I asked him, “Before I answer, I will ask you what this equation means?”. To which he was a bit flummoxed and just pointed at it. I said no, those are just symbols.

I explained to him that the left-hand side contained the acceleration following the fluid. The right-hand side contained the forces (viscous and the stress tensor) and the inclusion of the density term (mass). So it was a rewrite of Newton’s 2nd law of motion. Well, the then Director of Studies of Mathematics was also in attendance. During the coffee break, he sought me out for a chat two weeks later; an interview was set up, and the rest is history.

Navier-Stokes Fluid Mechanics Equation

So, after all that, one can see that the equation is Newton’s mass acceleration formula F = mdv / dt and not F = d(mv)/dt, which would be used in relativity. Stokes himself follows a long line of “Giants” in the prestigious position of Lucasian Professor of Mathematics. This is, arguably, the most famous chair in all Mathematics, including the likes of Newton, Airy, Babbage, Dirac, and Lighthill.
Returning to George, his work on fluid motion and viscosity led to his calculating the terminal velocity for a sphere falling in a viscous medium. I was fortunate to derive his law at UCL during my lectures on dimensional analysis. George also derived an expression for the drag force exerted on spherical objects with very small Reynolds numbers. He also has a beautiful integral formula named in his honor. The formula relates the normal component of the curl of a vector to the circulation comparable to the beauty in Gauss’ divergence theorem.

The Team keeps on Growing

I have not mentioned the other half of the tag team, i.e., Claude Louis Henri Navier (1785-36). He was taught Mathematics by the “Giant” J.Fourier (1768-30) whilst at the École Polytechnique. I have a friend at Oxford who tells me that he attended lectures by Dirac when he was at Trinity College. However, he mentions that he was not inspiring at all. This echoes the reports on Newton often, and he gave lectures to an empty class due to being such an appalling teacher. Navier can be found with his name “up in lights” on the Eiffel Tower, but that discussion is for another day.

P.A.M. Dirac – An Orchestrator of the Physics

Sci-Hub

Dr Vasos Pavlika

-

October 30, 2023

0

P.A.M. Dirac – An Orchestrator of the Physics

Dirac Equation

Where should one start to discuss the contribution of this Giant? Dirac started as an Engineer, graduating from Bristol University before moving to Cambridge, contributing (and initiating) quantum electrodynamics (QED), the Relativistic Quantum Field theory. In particle physics, the Dirac equation is a relativistic version of the Schrödinger equation. Dirac was looking for a linear equation, specifically guided by the Schrödinger equation, but that was relativistically invariant.
He could not find one that did not involve taking the square root of an operator. However, he devised a technique that allowed the linearisation that was required. However, this introduced a noncommutative algebra, from which he realized that the factors needed were matrices.
Determining the square root of an operator-led Dirac to consider both the positive and negative roots. Instead of conceding that there might be an error in his work. He proposed that these solutions must correspond to anti-matter (positron when considering the anti-particle of the electron).

Dirac, as Mathematics Professor at Cambridge

Dirac became the Lucasian Professor of Mathematics at Cambridge, arguably the most prestigious post in all of Mathematics, made famous by “Giants,” including I. Newton, C. Babbage, and G.G. Stokes.
I was fortunate to study the full equation of viscous flow in fluid dynamics that he is intimately involved with as one half of the Navier (1785-1836) – Stokes equation. Navier, by the way, can be found with his name “up in lights” (as it should be) as one of the legendary 72 names on the Eiffel Tower.

Dirac Preciseness

He was famous for his preciseness, and I often recount a famous event like this. While delivering a lecture at a conference, a member of the audience raised his hand and said:

“I don’t understand the equation on the top-right-hand corner of the blackboard.”
There was a silence in the room! After a long cessation, the session chair approached Dirac and quietly asked him if he wanted to answer the question.
“That was not a question; it was a comment – Dirac Replied.“
Dirac was brave enough to include matrices in his work. Matrices were just being admitted into mainstream Physics after the pioneering work of W. Heisenberg (1901-76) and before him by M.Born (1882-1970). On a related issue, matrices have their origins with the “Prince of Mathematics,” namely J.C.F.Gauss (1777-1855) and the Senior Wrangler, A. Caley (1821-95), but this is not the time to discuss them; I will have to wait for an appropriate date to do this.

Never ignore Negative Solutions

Let’s get things right. The positron was predicted by the great Mathematical Physicist P.A.M. Dirac (1902-84) when he was at St John’s, Cambridge, commencing his education as an Engineer at Bristol University. He took the bold step to NOT ignore the negative solution to the relativistic Schrodinger equation and predicted the anti-electron (now called a positron).
Dirac was mischievous rather like Euler (1707-83) when he (Euler) substituted $ix$ for (x) in the Maclaurin series expansion for (exp(x)), leading to Euler’s beautiful formula. A great book on Dirac is “The Strangest Man: The hidden Life of Paul Dirac, Quantum Genius” by Graham Farmelo.

Bernhard Riemann: Innovative Research in Topology

Sci-Hub

Dr Vasos Pavlika

-

October 29, 2023

0

Bernhard Riemann: Innovative Research in Topology

Riemann Surfaces and Research in Topology

Bernard Riemann surfaces, the Riemann function (for solving hyperbolic PDEs), and the Cauchy-Riemann equations in deriving an alternate physical plane where the independent variables are the stream function and a function analogous to the velocity potential function so that complex geometrical flow patterns are converted into ψ=constant and Φ=constant infinite rectangles so that I can set up my difference representations as well as integral formulae that can be used to solve any pseudo-Poisson equations. I also use Riemann’s advances in Analytic Continuation and much more.
I often mention to my students that if one wants to become a Mathematical “superstar” overnight, then prove the Riemann Hypothesis: that the Riemann zeta function has its zeros that are only the negative even integers and complex numbers with real parts equal to 1/2. Bernhard proposed this in 1859 and is now the “holy grail” of Mathematical pursuits, which will give instant immortality to its conqueror.

Bernhard Riemann Contribution in Mathematics

I have been fortunate in my academic career to teach the Riemann integral (as well as the Lebesgue (1875-41) integral) and Riemann sums. I often marvel at the expressions of my students when they see that the integral of polynomials can easily be obtained using the well-known formulae for the sum of polynomials (which I also derive but not by induction) and Riemann sums.

Riemannian geometry

Riemann also founded Riemannian geometry in 1854 after Gauss (1777-55) asked him (as Riemann was his student), to prepare a Habilitationsschrift on the foundations of geometry, and this set the stage for Einstein’s (1879-55) general theory of relativity.

Riemannian geometry is a consistent non-Euclidean geometry (meaning that the fifth postulate of Euclid is relaxed); this step took centuries to occur due to the reverence held for Euclid’s (300 BC) work. Another such consistent geometry is that of Lobachevsky (1792-56).

Remembering Bernhard Riemann

I want to relay a little anecdote about Riemann and Gauss that I have been stating throughout my teaching career, spanning over 35+ years. When discussing Riemann, I always say to my students that it must have been very daunting for him to have Gauss as his Ph.D. advisor, only for one of my students at Oxford during a class reply, “It must have been scary for Gauss to have Riemann as his student.” That comment made me look at things from a completely different perspective (being a fan of Gauss, of course). As soon as I finished my Ph.D. and had more time on my hands, I purchased Gauss’ masterpiece Disquisitiones Arithmeticae (Latin “Arithmetical Investigations”), which deals with his passion for the primes and number theory, and this is a very interesting read.

I will end this discussion by stating how Stern (1807-94) described Riemann after he read Legendre’s (1752-33) masterpiece:

… “he already sang like a canary.”

Alas, I have run out of space again. Sorry, “old friend”.

Web Scraping with Python: Techniques and Best Practices

Artificial Intelligence

Syeda Umme Eman

-

October 29, 2023

0

Web Scraping with Python: Techniques and Best Practices

Introduction:

Python is very popular in web development because of its simplicity and readability. With abundant frameworks and packages, Python has emerged as the preferred option for creating scalable and reliable online applications. This article will cover all facets of Python web programming, from frontend to backend, and introduce some of the most well-known frameworks and tools on the market.

Backend Development

1. Django:

The high-level Python web framework Django called the “batteries-included” framework, promotes quick development and simple, straightforward design. It offers every tool needed to create a web application, such as an admin interface, authentication, an ORM (Object-Relational Mapping) framework, and much more. Large-scale applications can benefit greatly from Django’s scalability and adherence to the DRY (Don’t Repeat Yourself) principle.

2. Flask:

The building blocks for creating web applications are provided by the lightweight and tiny web framework Flask. Flask is more adaptable than Django, enabling developers to select and incorporate particular components to the needs of their projects. RESTful APIs and smaller projects are good fits for it. Flask is a well-liked option among developers due to its simplicity and ease of learning.

Frontend Development

3. JavaScript and Frontend Libraries/Frameworks:

JavaScript is the preferred language for frontend development, while Python is mainly used for backend development. Using JavaScript libraries and frameworks like React, Angular, or Vue.js to create dynamic and interactive user interfaces is a common practice in modern web development.

Data Handling and Databases

4. SQLAlchemy:

For Python, SQLAlchemy is a robust and adaptable ORM package. Rather than working with raw SQL queries, developers can deal with Python objects thanks to its high-level interface for communicating with databases. Because SQLAlchemy supports a large number of database systems, programmers can use it for a variety of project kinds.

5. Django ORM:

The integrated ORM system in the Django framework is a potent tool for database management for developers. It makes database operations simpler and enables Pythonic model and query set manipulation for developers. Numerous database backends, such as PostgreSQL, MySQL, SQLite, and Oracle, are supported by the Django ORM.

APIs and Microservices

6. Django REST framework:

The preferred option for constructing resilient APIs in Django is the Django REST framework (DRF). DRF offers a robust toolkit for building Web APIs that simplify the handling of authentication, data serialization and deserialization, and implementation of many API views. It guarantees maintainability and scalability by adhering to the RESTful API design standards.

Testing

7. PyTest:

PyTest is a well-liked Python testing framework that makes developing and running tests easier. Because of its clear and basic syntax, developers may easily write extensive test suites for their web applications.

Deployment and Hosting

8. Heroku:

Heroku is a cloud platform that makes maintaining, scaling, and delivering web applications easier. It offers smooth deployment and supports various programming languages, including Python. Heroku is a great option for hosting Python web applications because of its extensive ecosystem of connectors and add-ons.

Conclusion

Because of its adaptability and abundance of libraries and frameworks, Python has become a major force in the web development industry. Python offers the resources and tools required to complete the task quickly and effectively, regardless of the size of the system you’re developing—from a simple web application to a sophisticated enterprise-level solution. Developers may build web applications that are scalable, reliable, maintainable, and simple to expand by utilizing Python’s capabilities. Launch your projects into new possibilities by delving into Python web programming.

Heike Kamerlingh Onnes: The Unsung Hero of Physics

Sci-Hub

Dr Vasos Pavlika

-

October 28, 2023

0

Heike Kamerlingh Onnes: The Unsung Hero of Physics

Unsung Dutch Hero

Heike Kamerlingh Onnes studied under two well-known “Giants”, Robert Bunsen (1811-99) and Gustav Kirchhoff (1824-77) at the University of Heidelberg from 1871 to 1873. I must digress here and discuss Kirchoff with his circuit laws that I recall using as a young undergraduate Mathematics and Physics student. His so-called first law states that for any node (point in a circuit):

The algebraic sum of currents in a network of conductors meeting at a point is zero.

Shaping of Modern Physics

This is a conservation law in Physics (in this case of charge) and whenever I read about conservation laws in Physics I am always instantly reminded of one of the greatest ever female Mathematicians/Physicists in this case of E.Noether (1882-35) who was taught by other “Giants” of Mathematics in Göttingen Germany when Göttingen was the centre and powerhouse of Mathematics and Physics in the world and which during its history can boast the presence of Gauss (1777-55), Dirichlet (1805-55), Hilbert (1862-43) and Minkowski (1864-09) who by the way called Einstein (1879-55) “an idle dog” due to his lack of participation during his lectures.

In fact, Noether explained facets of Einstein’s General Theory of Relativity to Hilbert and Klein (1849-25). She also made huge contributions to the Calculus of Variations, which I am fortunate to introduce at UCL on a second-year Mathematical Economics module that I deliver and which includes the application of the Euler-Lagrange equation.

Discovering Superconductivity

Returning to Onnes, he discovered superconductivity which essentially is the flow of electric charge in which there is an almost complete disappearance of resistance and occurs at temperatures near absolute zero 0K, the temperature of occurrence we call the characteristic temperature. For this work, Onnes was awarded the 1913 Nobel Prize in Physics. Onnes was also greatly influenced by Van der Waals (1837-23), who derived the equation of state for real fluids, and this equation approximates the behaviour of real fluids (in which viscous forces are present) above their critical temperatures.

Further Contributions to Physics

Onnes was also influenced by another one of his compatriots, Hendrik Lorentz (1853-28), and scholars today admit that Lorentz, as well as Poincaré (1854-12) developed the Mathematics of Special Relativity, and originally the theory was referred to as the “Lorentz–Einstein theory”, but it is argued that it was Einstein who eliminated the classical ether and demonstrated the relativity of space and time taking further Newton’s (1643-27) and Galileo’s (1564-42) ideas in these respective areas. I recall reading about Poincare as an undergraduate when I realized that he was responsible for advancing the theories associated with perturbations and chaos, disciplines that I became very interested in as a graduate student.

Alas, I have run out of space again. Until next time, “old friend”.

Michael Faraday: Pioneer in Electrical Science and Technology

Dr Vasos Pavlika

-

October 28, 2023

0

Michael Faraday: Pioneer in Electrical Science and Technology

Foundation of Electric Motor Technology

Where does one start when discussing this “Giant”? With little formal education, Faraday discovered the underlying principles of electromagnetic induction and electrolysis. His inventions of electromagnetic rotary devices formed the foundation of electrical motor technology, and it was largely due to his efforts that electricity became practical for use in technology. It is well known that Faraday’s Mathematical abilities were no match for those of James Clerk Maxwell (1831-79), who took Faraday’s discoveries and expressed them in what we refer to today as Maxwell’s equations (there are four equations, but Maxwell originally stated twenty however it was Oliver Heaviside (1850-25) that reduced them to the four that we have today).

Legacy of Micheal Faraday

Faraday was the idol of many “Giants” who followed him, including A. Einstein (1879-55), who was said to have kept a photograph of him, and Maxwell, who himself praised Faraday’s latent Mathematical skills after the idea of field lines were introduced by him. One of Faraday’s laws relates to the rate at which these lines are “cut”. Furthermore, “Papa” Ernest Rutherford (1871-37), who likewise was a great experimentalist, paid homage to Faraday, stating:

“When we consider the magnitude and extent of his discoveries and their influence on the progress of science and industry, there is no honour too great to pay to the memory of Faraday, one of the greatest scientific discoverers of all time.” E. Rutherford.

Personal Beliefs and Principles

Faraday, a pioneer in the field of electrical science later turned down a knighthood based on his strict Biblical beliefs (he was a devout Christian). He was not the first “Giant” to refuse such an accolade; one who comes immediately to mind is Stephen Hawking (1942-18), who refused the honour due to being an opposer of the monarchy. I recall that R. Feynman (1918-88), during his interview on Horizon, demonstrated a similar disdain for receiving awards for his work.

In my opinion, the most famous occasion of a “Giant” refusing an award on account of his work was when Grigori Perelman (1966-) turned down the Fields Medal for his work that led to the solution to the Poincaré (1854-12) conjecture using Ricci flow, he turned down the prize after falling out of love with academia, in fact he presented his solution to the problem by posting it on arXiv and not in a reputable journal.

Conclusion

Returning to Faraday, he also made great contributions to Chemistry. His earliest chemical work was to assist Humphry Davy (1778-29), who, as is no doubt well known, was a pioneer of electrolysis and who was able to split many ionic compounds and thus separate several elements. Faraday was involved in the study of chlorine; he discovered two new compounds of it and carbon. He also conducted the first rough experiments on the diffusion of gases, a phenomenon that was further elucidated by Graham (1805-69).

Alas, once again, I have run out of space, sorry “Old friend”.

Code Your Way to Efficiency: Task Automation with Python

Artificial Intelligence

Syeda Umme Eman

-

October 28, 2023

0

Code Your Way to Efficiency: Task Automation with Python

Introduction:

Automation is now essential to productivity and efficiency in today’s fast-paced digital world. Python is a popular choice for task automation since it is a robust and versatile programming language. Python offers a vast range of libraries and tools that enable automation for individuals and enterprises, ranging from file management and data processing to web scraping and system administration.

Why Python for Automation?

Python is quite popular in automation for several important reasons:

1. Simplicity and Readability:

Python requires less time and effort for automation projects because of its simple syntax and natural language structures, which make it easier to learn and write.

2. Cross-Platform Compatibility:

Python has extensive applications due to its compatibility with a wide range of software and hardware and its ability to run on major operating systems such as Windows, macOS, and Linux.

3. Large Ecosystem:

Python has an abundance of libraries and modules covering a wide range of activities, such as data manipulation (Pandas), GUI automation (PyAutoGUI), and web scraping (Beautiful Soup, Requests).

4. Active Community and Support:

A vibrant development community exists for Python, which contributes to its vast documentation, hosts forums for support, and produces third-party packages that expand its functionality.

Common Automation Tasks with Python

1. File Operations:

File Copying/Moving: Automate copying or transferring files from one directory to another.
File Renaming: Rename files in bulk according to a predetermined pattern or criteria.
File deletion: Get rid of files that are more than a specified age or have particular characteristics.

2. Data Processing:

CSV/Excel Manipulation: Read, write, and alter data stored in CSV or Excel files. For this, libraries like Pandas are really helpful.

3. Web Scraping Data Extraction:

Data Extraction: Use libraries like Requests and Beautiful Soup to extract data from websites for reporting, analysis, or archive reasons.

4. Automating Interactions with GUIs:

Automated Testing: Use tools like PyAutoGUI or Selenium to automate the testing of graphical user interfaces.

5. Planned Assignments:

Cron Jobs (Linux) / Task Scheduler (Windows): Utilise Python scripts in conjunction with system scheduling capabilities to carry out tasks at certain periods or intervals using Cron Jobs (Linux) or Task Scheduler (Windows).

6. Email Automation:

Sending Emails: Use libraries such as smtplib to automate email sending for notifications, reports, and other types of communication.

7. System Administration:

Handling Services: Initiate, cease, or resume a system’s services.
Log Parsing: Parse logs to look for particular faults or events.

8. Database Operations:

Data Extraction/Loading: Automate database-related processes, like loading data from outside sources or extracting data for reporting.

Getting Started with Python Automation:

1. Install Python:

Utilizing the official Python website (https://www.python.org/), download and install Python. Please ensure that Python is added to your system’s PATH when installing it.

2. Select a Text Editor or IDE:

IDLE, Jupyter Notebook, PyCharm, and Visual Studio Code are popular options.

3. Study the fundamentals of Python:

Learn the basic ideas of Python, including variables, loops, conditionals, and functions.

4. Examine Libraries of Automation:

Learn about libraries such as shutil, requests, os, and others according to the jobs you wish to automate.

5. Practice and Experiment:

Build up more complicated automation projects gradually by starting with smaller, more manageable activities.

6. Utilize Version Control:

Track changes and work with colleagues on automation projects by collaborating with version control systems like Git.

Best Practices for Python Automation:

Error Handling: To foresee and handle possible problems during automation, use strong error handling.
Logging and Reporting: Create logs to monitor the execution of your scripts and generate reports that simplify monitoring and analysis.
Modularize Your Code: To improve maintainability and reusability, divide your scripts into functions or modules.
Documentation: To make your code easier to understand for both you and other people, include comments and documentation that describe its functionality and goal.
Security considerations: Use caution while working with private information or sensitive processes, and adhere to secure coding best practices.

Conclusion:

In conclusion, Python automation enables people and organizations to automate repetitive processes, save time, and boost productivity. Python’s broad library ecosystem and versatility allow you to automate many jobs, from basic file operations to intricate system administration. You can reach new heights of productivity in your work and projects by mastering Python automata with commitment, practice, and adherence to best practices.

Masketer

Masketer

Masketer

Company

Masketer

Masketer

Introduction: